The tool expects the input to be written to stdin in the xmts file format, which is described here: xmts-specification, and outputs the result to stdout. A simple example of the textual representation of an input system is here and more can be found in the downloaded package.
The algorithm is selected via the -a flag and additional parameters can be passed via the -p
flag. The initial states are passed to the algorithms as starting
points. Furthermore the arity and supported types of an algorithm can be
queried by passing -q.
Currently the following algorithms are exposed via the command-line interface.
CompositionDMTS(Parameters: synchronising alphabet for the two systems)CompositionMTS(Parameters: synchronising alphabet for the two systems)ConjunctionConsistencyDeterministicHullBMTSDeterministicHullMTSLTLChecker(Parameters: LTL Formula to be checked)MaxImplementationModalRefinementFixedPointModalRefinementQSatQuotient
Examples
Query Algorithm Information
[motras-algorithms]$ java -jar motras-algorithms.jar -q -a ModalRefinementQSat Arity: 2 Supported Types: [mts, dmts, bmts, pmts]
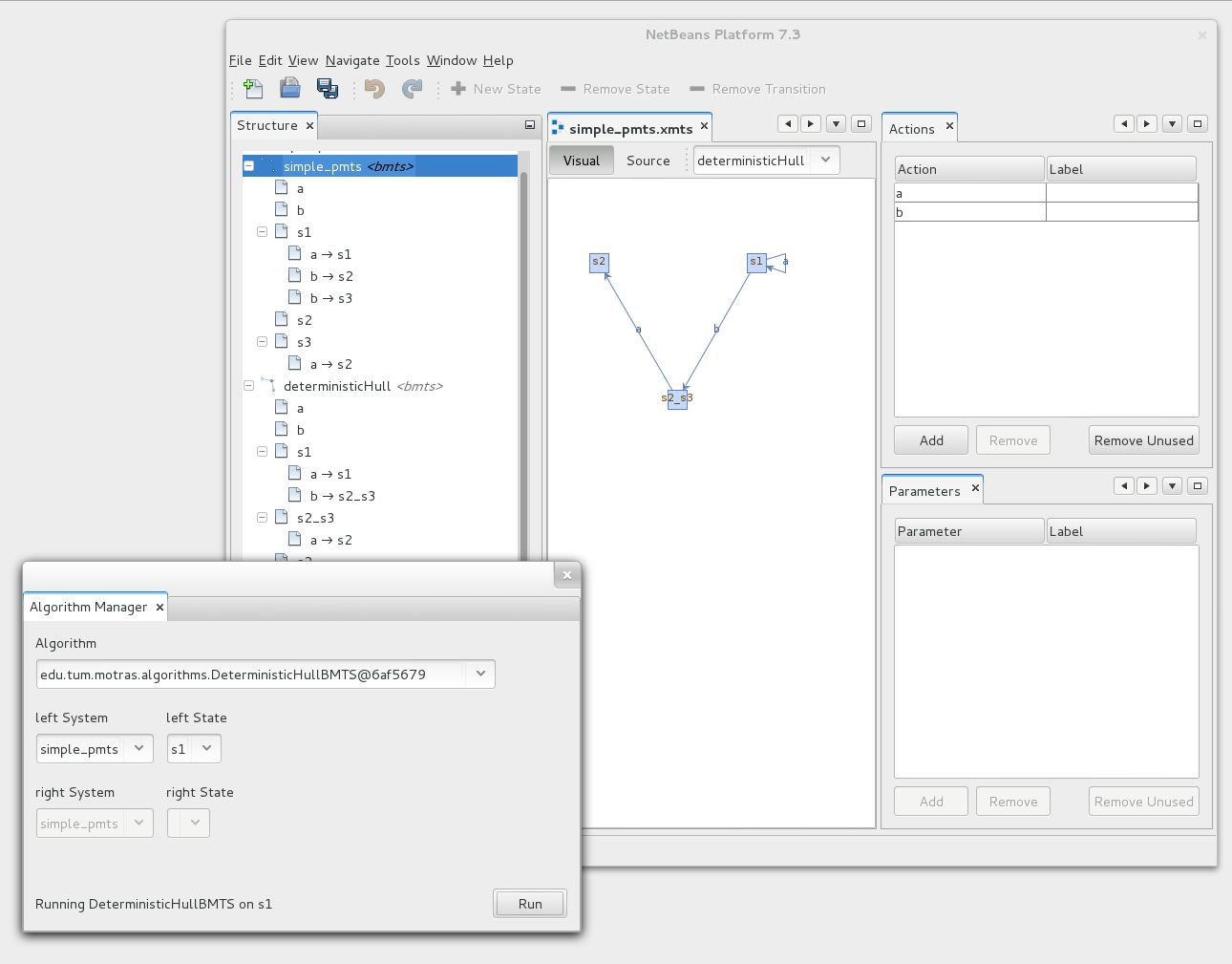
Constructing the Deterministic Hull (MTS Version)
Let's assume the following transition system is saved in the file non_deterministic_mts.xmts.
mts non_deterministic_mts [ initial_state s1 action a action b state s1 [ obligation a.s2 & b.s3 a -> s2 a -> s3 b -> s3 ] state s2 [ b -> s4 ] state s3 [ a -> s3 a -> s2 ] state s4 ]
The deterministic Hull is simply created by piping the file to stdin of the tool.
[motras-algorithms]$ cat non_deterministic_mts.xmts | java -jar motras-algorithms.jar -a DeterministicHullMTS
Which then yields the following result.
mts deterministicHull[ initial_state s1 action b action a state s1[ obligation (b.s3 & a.s2_s3) b -> s3 a -> s2_s3 ] state s3[ a -> s2_s3 ] state s2_s3[ b -> s4 a -> s2_s3 ] state s4 ]
Checking Modal Refinement
We now check modal refinement on two systems contained in the traffic examples directory.
[motras-algorithms]$ cat simple1.xmts param2.xmts | java -jar motras-algorithms.jar -a ModalRefinementQSat true [motras-algorithms]$ cat simple1.xmts simple2.xmts | java -jar motras-algorithms.jar -a ModalRefinementQSat false
Checking a LTL Formula
This example is taken from here.
[motras-algorithms]$ cat CoffeeAndTeaDMTS.xmts | java -jar motras-algorithms.jar -a LTLChecker -p "G ! coffee" true
 homepage!
homepage!